00. 탄소 분율에 기반한 철강재료의 인장시험곡선 시뮬레이션
철강에서의 탄소조성의 변화에 따른 구성 조직의 변화는 재료의 강도를 결정짓는 중요한 기구이다. 이러한 강화기구는 탄소함유량의 증가에 따른 펄라이트의 분율 변화에 크게 의존한다. 이러한 분율의 변화는 Fe-Fe3C 상태도에서 통하여 계산 가능하다. 이를 이용하여 실제 조직시험을 통해 페라이트와 펄라이트의 조직의 경도를 측정하고, 이러한 경도가 강도에 1차원적으로 영향을 준다면, 탄소조성을 통하여 강도의 변화를 예측할수있으며, 실제 아래와 같은 그림의 변화를 보인다.

따라서 아래의 이론적 가정들에 의하여, 탄소분율변화에 따른 철강재료의 물성변화를 예측하여볼수있다.
1. 오직 탄소의 함유량의 증가에 금속조직의 변화에 따라 철강의 강도(경도)가 변한다고 가정함. (결정립미세화 강화효과, 고용체강화효과, 열처리에 의한 조직변화, 가공경화에 의한 전위증가에 의한 강화효과 등을 포함한 다른 강화 효과는 고려하지않는다.)
2. 탄소의 범위는 0.00~2.1wt%C로 제한한다 (순철 ~ 강의 범위, 페라이트, 펄라이트, 시멘타이트 조직만 존재한다고 가정하기 위함임.)
3.재료의 항복점의 연신률은 0.005%로 항상 일정하다고 가정한다.
4. 금속의 조직은 충분히 nomalization 되어 표준조직을 가진다고 가정한다.
5. (아공석 영역에서)강도와 경도는 직선형태의 비례를 가진다.
프로그램의 다이어그램은 아래와 같다.
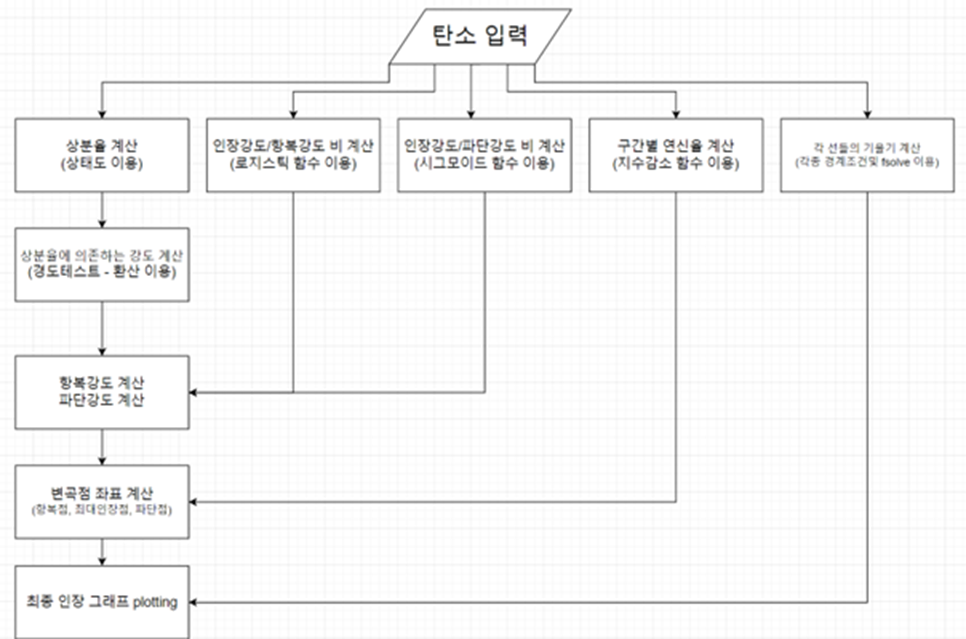
아래는 실제 프로그램이다. 누구나 자유롭게 이용해도 좋다. 그 외에 프로그램의 자세한 설명은 위의 문서를 올리니 필요하다면 참고해도 좋다.
실제 프로그램
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
class CarbonSteel:
def __init__(self, carbon_content):
self.carbon_content = carbon_content
self.pearlite_percent = 0 #펄라이트분율
self.a_percent = 0 #페라이트분율
self.cementite_percent = 0 #시멘타이트분율
self.yield_strength = 0 #항복강도
self.tensile_strength = 0 #인장강도
self.fracture_strength = 0 #파단강도
self.yield_to_tensile_elongation = 0
self.tensile_to_fracture_elongation = 0
self.tensile_elongation_point = 0 # 최대 인장점의 변형률
self.fracture_elongation_point = 0 # 파단점의 변형률
self.E = 0 # 탄성 계수
self.K = 0 # 강화 계수
self.n = 0 # 강화 지수
self.a2 = 0 #네킹구간계수 a2
self.b2 = 0 #네킹구간계수 b2
self.c2 = 0 #네킹구간계수 c2
self.yield_elongation_point = 0.005 # 항복시 변형률은 상수로 가정
self.YT_ratio = 0
self.FT_ratio = 0
self.calculate_structure() #분율계산
self.calculate_properties() #물성계산
def calculate_structure(self):
"""Fe3C 상태도에 의한 각 상의 분율 계산"""
if self.carbon_content <= 0.76: # 아공석강의 분율 계산
self.pearlite_percent = ((self.carbon_content - 0.022) / 0.738) * 100
self.a_percent = ((0.76 - self.carbon_content) / 0.738) * 100
elif self.carbon_content <= 2.1: # 과공석강의 계산
self.cementite_percent = ((self.carbon_content - 0.76) / 5.91) * 100
self.pearlite_percent = ((6.67 - self.carbon_content) / 5.91) * 100
else:
# 범위를 벗어난 경우 처리
print("범위를 벗어났습니다!")
def calculate_properties(self):
"""탄소 함유량에 따른 물성 계산"""
# 상수 정의
pearlite_tensile = 903
a_tensile = 490
cementite_tensile = 30
# YT_ratio와 FT_ratio 계산
self.YT_ratio = self.get_yield_and_tensile_strength_ratio()
self.FT_ratio = self.get_fracture_and_tensile_strength_ratio()
# 각 상의 분율에 따른 인장강도 계산
self.tensile_strength = (pearlite_tensile * self.pearlite_percent / 100) + \
(a_tensile * self.a_percent / 100) + \
(cementite_tensile * self.cementite_percent / 100)
# YT_ratio와 FT_ratio를 사용하여 항복강도와 파단강도 계산
self.yield_strength = self.YT_ratio * self.tensile_strength
self.fracture_strength = self.FT_ratio * self.tensile_strength
#연신율 계산
self.yield_to_tensile_elongation = self.yield_and_tensile_elongation(self.carbon_content) / 100
self.tensile_to_fracture_elongation = self.tensile_and_fracture_elongation(self.carbon_content) / 100
#연신포인트계산
self.tensile_elongation_point = self.yield_elongation_point + self.yield_to_tensile_elongation
self.fracture_elongation_point = self.tensile_elongation_point + self.tensile_to_fracture_elongation
#탄성계수,가공경화지수,계수 계산(E,K,n)
self.E, self.K, self.n = self.find_k_n(self.yield_strength, self.tensile_strength,self.yield_elongation_point, self.tensile_elongation_point)
#네킹구간 곡선계수 계산
self.find_necking_curve_coefficients()
###아래의 함수는 수학적 연산을 위한 함수임.
def get_yield_and_tensile_strength_ratio(self):
"""인장강도와 항복강도 비율 계산"""
k = 1.4409794871081625
x0 = -0.2111867818566157
L = 1
return L / (1 + np.exp(-k * (self.carbon_content - x0)))
def get_fracture_and_tensile_strength_ratio(self):
"""인장강도와 파단강도 비율 계산"""
k = 1.4409794871081625
x0 = -0.2111867818566157
L = 0.4
return 0.6 + L / (1 + np.exp(-k * (self.carbon_content - x0)))
def tensile_and_fracture_elongation(self, x):
"""탄소 함유량(x)에 따른 네킹 구간의 연신율을 반환하는 함수"""
k = -2.52
return 25 * np.exp(k * x)
def yield_and_tensile_elongation(self, x):
"""탄소 함유량(x)에 따른 소성 구간의 연신율을 반환하는 함수"""
k = -3.2
return 24.2 * np.exp(k * x)
def find_k_n(self, elastic_stress, ultimate_stress, elastic_strain, ultimate_strain):
def ramberg_osgood_equations(p):
E, K, n = p
eq1 = E * elastic_strain + K * elastic_strain**n - elastic_stress
eq2 = E * ultimate_strain + K * ultimate_strain**n - ultimate_stress
eq3 = E + n * K * ultimate_strain**(n - 1) # The slope at the ultimate point is 0
return (eq1, eq2, eq3)
initial_guess = [-1000, 1000, 0.1] # 초기 추정값
E_opt, K_opt, n_opt = fsolve(ramberg_osgood_equations, initial_guess)
return (E_opt, K_opt, n_opt)
def find_necking_curve_coefficients(self):
def necking_curve_equations(p):
a2, b2, c2 = p
eq1 = a2 * self.tensile_elongation_point**2 + b2 * self.tensile_elongation_point + c2 - self.tensile_strength
eq2 = a2 * self.fracture_elongation_point**2 + b2 * self.fracture_elongation_point + c2 - self.fracture_strength
eq3 = 2 * a2 * self.tensile_elongation_point + b2 # 시작점에서의 미분값이 0
return (eq1, eq2, eq3)
initial_guess = [1, 1, 1] # 초기 추정값
self.a2, self.b2, self.c2 = fsolve(necking_curve_equations, initial_guess)
def plot_stress_strain_curve(self):
"""
스트레스-스트레인 곡선을 그리는 메서드
"""
# 탄소 함량에 따른 조건부 분기
if self.carbon_content > 1.2: # 특정 탄소 함량 이상일 경우
# 선형 곡선 그리기
plt.plot([0, self.tensile_elongation_point], [0, self.tensile_strength], color='red', label='Linear Section')
else:
# 비선형 곡선 그리기
x_curve = np.linspace(0, self.tensile_elongation_point, 5000)
y_curve = self.E * x_curve + self.K * x_curve**self.n
plt.plot(x_curve, y_curve, color='red', label='Elastic - Plastic Section')
# 네킹 구간 모델링 (시작점부터 끝점까지)
x_necking = np.linspace(self.tensile_elongation_point, self.fracture_elongation_point, 500)
y_necking = self.a2 * x_necking**2 + self.b2 * x_necking + self.c2
plt.plot(x_necking, y_necking, color='orange', label='Necking Section')
# 그래프 설정
plt.title('Stress-Strain Curve with Non-Linear Model')
plt.xlabel('Strain')
plt.ylabel('Stress (MPa)')
plt.xlim(-0.005, 0.5)
plt.ylim(0, 1000)
plt.grid(True)
plt.legend()
# 탄소 함유량에 따른 여러 곡선을 그리기 위한 함수
def plot_multiple_carbon_steel_curves(carbon_contents):
plt.figure(figsize=(10, 8))
for i in carbon_contents:#인장시험 그래프 그리는 반복문
steel = CarbonSteel(i) #클래스 생성하기
steel.plot_stress_strain_curve() #그리기
"""설정값"""
plt.title('Stress-Strain Curves for Various Carbon Contents')
plt.xlabel('Strain')
plt.ylabel('Stress (MPa)')
plt.grid(True)
plt.legend()
plt.show()
carbon_percent = []
while True:
input_data = input("탄소함유량을 입력해주세요 :")
if input_data == "stop":
break
else:
carbon_percent.append(float(input_data))
print("그만 입력하실려면 stop을 입력해주세요.")
plot_multiple_carbon_steel_curves(carbon_percent)
for i in carbon_percent:
steel = CarbonSteel(i)
print(i, "%", "탄소의 성질")
print(f"펄라이트 비율: {steel.pearlite_percent:.2f}%, 페라이트 비율: {steel.a_percent:.2f}%, 시멘타이트 비율: {steel.cementite_percent:.2f}%")
print(f"항복강도: {steel.yield_strength:.2f}, 인장강도: {steel.tensile_strength:.2f}, 파단강도: {steel.fracture_strength:.2f}, YT:{steel.YT_ratio:.2f}, FT:{steel.FT_ratio:.2f}")
print(f"항복에서 인장까지 연신율: {steel.yield_to_tensile_elongation:.3f}, 인장에서 파단까지 연신율: {steel.tensile_to_fracture_elongation:.3f}")
print(f"E: {steel.E:.2f}, K: {steel.K:.2f}, n: {steel.n:.2f}")
print(f"a2: {steel.a2:.2f}, b2: {steel.b2:.2f}, c2: {steel.c2:.2f}")
print("\n")


결론
해당 프로그램은 매우 이상적인 상황을 가정하여 작성되었기에 산업적으로 유용하지는 않다. 또한 항복강도와 최대인장강도의 관계성이 있는지에 대해서도 명확하지 않다. 하지만 경도시험을 통하여 경도를 측정하고, 이를 통해 인장강도를 측정한뒤 실제 인장실험을 해본다면 재료와 환경의 컨트롤이 가능한 실험적인 영역에서는 해당 그래프를 참조하여 그래프와의 차이를 분석함으로서 다른 강화기구의 영향성(결정립 강화기구이외의) 영향을 일부 알 수 있다.